

Look at the table below to understand the formula behind the volume of various prisms: Shape Thus, the unit of volume of the prism is given as V = (units 2) × (units) = units 3. The base area is given in (units 2) and the height of the prism is given in (units). Thus, the volume of a prism is represented as V = B × H where "V" is the volume, "B" is the base area, and "H" height of the prism. The volume of a prism is the product of the area of the base and height of the prism. The volume of a prism is defined as the total amount of space or vacuum a prism occupies. Surface area of octagonal prism = 4a 2 (1 + √2) + 8aH


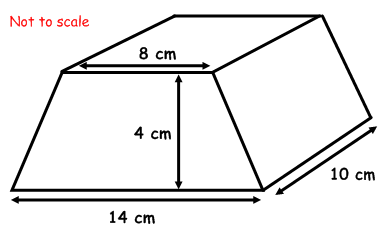
Surface area of regular hexagonal prism = 6ah + 3√3a 2 Surface area of hexagonal prism = 6b(a + h) Surface area of pentagonal prism = 5ab + 5bh Surface area of trapezoidal prism = h (b + d) + l (a + b + c + d) Surface area of rectangular prism = 2(lb + bh + lh) Surface area of square prism = 2a 2 + 4ah Surface area of triangular prism = bh + (s1 + s2 + b)H Surface Area of Prisms = (2 × Base Area) + (Base perimeter × height) See the table below to understand this concept behind the surface area of various prisms: Shape The bases of different types of prisms are different so are the formulas to determine the surface area of the prism. There are seven types of prisms we read above based on the shape of the bases. The total surface area of a prism = Lateral surface area of prism + area of the two bases = (2 × Base Area) + Lateral surface area or (2 × Base Area) + (Base perimeter × height).
The lateral surface area of prism = base perimeter × height The lateral area of a prism is the sum of the areas of all its lateral faces whereas the total surface area of a prism is the sum of its lateral area and area of its bases. There are two types of areas we read about, first, the lateral surface area of the prism, and second, the total surface area of the prism. Let us learn these two in the case of prisms. The two formulas are the area of the shape and volume of the shape. There are two basic formulas we read in geometry about all the respective 3-dimensional shapes.
Trapezoidal Prism: A prism whose bases are trapezoid in shape is considered a trapezoidal prism. Octagonal Prism: A prism whose bases are octagon in shape is considered an octagonal prism. Hexagonal Prisms: A prism whose bases are hexagon in shape is considered a hexagonal prism. Pentagonal Prism: A prism whose bases are pentagon in shape is considered a pentagonal prism. Rectangular prism: A prism whose bases are rectangle in shape is considered a rectangular prism (a rectangular prism is cuboidal in shape). Square Prism: A prism whose bases are square in shape is considered a square prism. Triangular Prism: A prism whose bases are triangle in shape is considered a triangular prism. Oblique Prism: An oblique prism appears to be tilted and the two flat ends are not aligned and the side faces are parallelograms.Ī prism is named on the basis of the shape obtained by the cross-section of the prism. Right Prism: A right prism has two flat ends that are perfectly aligned with all the side faces in the shape of rectangles. There are two different prisms based on the alignment of the bases named: Prisms Based on the Alignment of the Identical Bases. Irregular Prism: If the base of the prism is in the shape of an irregular polygon, the prism is an irregular prism. Regular Prism: If the base of the prism is in the shape of a regular polygon, the prism is a regular prism. There are two types of prisms in this category named as: Prisms can be classified on the following basis: Prisms Based on the Type of Polygon, of the BaseĪ prism is classified on the basis of the type of polygon base it has. For example, if you are starting with mm and you know r and h in mm, your calculations will result with V in mm 3 and S in mm 2.īelow are the standard formulas for surface area.Before reading about various types of prisms let us understand on what basis types of prisms can be obtained. The units are in place to give an indication of the order of the results such as ft, ft 2 or ft 3. Units: Note that units are shown for convenience but do not affect the calculations. Online calculator to calculate the surface area of geometric solids including a capsule, cone, frustum, cube, cylinder, hemisphere, pyramid, rectangular prism, sphere, spherical cap, and triangular prism








 0 kommentar(er)
0 kommentar(er)
